Research

Digital Twins
Digital twins are becoming an increasing essential component in the design and management of assets in modern industry and engineering, with widespread use in civil engineering, the energy and aerospace sectors. Despite the diversity of application areas, there are common challenges faced by each which fall within the remit of: computational statistics, uncertainty quantification, the analysis and approximation of partial differential equations (PDEs), AI, and machine learning. These challenges relate to the fundamental question of how to systematically combine data with physics-based models in the creation of digital twins, and how then to correctly incorporate digital twins within a risk-stratified decision-making pipeline. The overarching goal of this project is to identify fundamental challenges faced in the development of digital twins for complex engineering systems, and by leveraging recent developments in applied mathematics, computational statistics and machine learning develop generally applicable methodology which can be used to address these challenges.
Read more
Monte Carlo Methods
Monte Carlo methods have revolutionnised statistical computation by allowing for efficient simulation from probability distributions, and efficient numerical integration against these distributions. Recent contributions from the group leader, Mark Girolami, include methodological developments in these areas: 1) Hamiltonian Monte Carlo methods, 2) Control variates and functionals.
Read more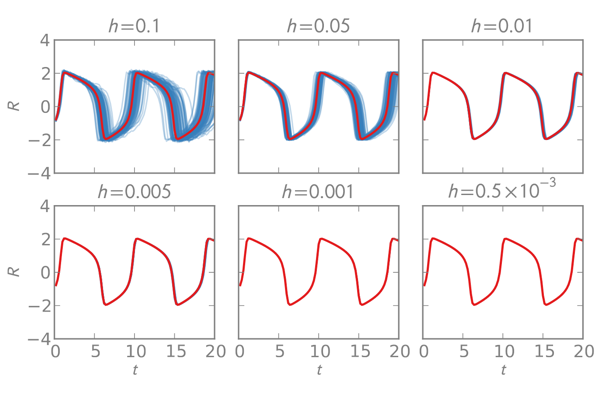
Probabilistic Numerics
Probabilistic numerical methods are a set of tools to solve numerical analysis problems from the point of view of statistical inference. Our work mostly focuses on Bayesian numerical methods, which are motivated by their uncertainty quantification properties for the output of numerical methods. The group has significantly advanced the field in research years, with work on the foundations of probabilistic numerics, on methodology for quadrature, ODE solvers and PDE solvers, and on applications to complex engineering problems.
Read moreInsights into Cities
ICONIC aims to develop theory, methodology, and algorithms to propagate uncertainty in mathematical models of socio-economic phenomena in future cities. Funded by a 5-year, £3M EPSRC programme grant, this project brings together a research team with the appropriate combination of skills in modeling, numerical analysis, statistics and high performance computing. Acknowledging that urban analytics is a very fast-moving field where new technologies and data sources emerge rapidly, and exploiting the flexibility built into an EPSRC programme grant, we apply the new tools to related city topics concerning human mobility, transport and infrastructure. In this way, the project enhances the UK’s research capabilities in the fast-moving and globally significant Future Cities field.
Read more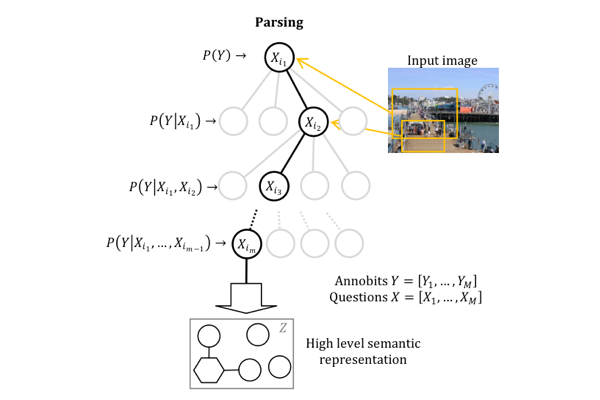
Semantic Information Pursuit for Multimodal Data Analysis (MURI)
In 1948 Shanon laid the foundations of information theory which revolutionized statistics, physics, engineering, and computer science. A strong limitation, however, is that the semantic content of data is not taken into account. This research will produce a novel framework for characterizing semantic information content in multimodal data. It will combine non-convex optimization with advanced statistical methods, leading to new representation learning algorithms, measures of uncertainty, and sampling methods. Given data from a scene, the algorithms will be able find the most informative representations of the data for a specific task. These methods will be applied to complex datasets from real situations, including text, images, videos, sensor signals, and cameras, resulting in intelligent decision based algorithms. Our group is working on characertizing uncertainty in multimodal representations. We will develop a statistical framework for characterizing the uncertainty of the information representations using both frequentists and Bayesian approaches. We will also develop efficient statistical sampling methods, which will be useful for both characterizing uncertainty and performing inference in the information pursuit framework.
Read more