Monte Carlo Methods
Table of contents:
Control Functionals
Control functionals for Monte Carlo Integration
Monte Carlo integation attempts to estimate an expectation of a function of a random variable, based on a collection of independent realisations. The most basic solution to this problem is to construct an ‘‘arithmetic mean’’ estimator. Under the central limit theorem, the arithmetic mean converges to its expectation at a rate \(O(n^{-1/2})\), where n is the number of independent realisations. However in many modern applications, e.g. involving complex computer models, root-n convergence is simply too slow. In a recent paper, Chris Oates, Mark Girolami and Nicolas Chopin introduced a new class of estimators for Monte Carlo integration that leverage gradient information on the sampling distribution in order to improve performance. The proposed estimators, called ‘‘control functionals’’, achieve super-root-n-convergence and often require orders of magnitude fewer simulations, compared with existing approaches, in order to achieve a fixed level of precision.
Our methodology, called ‘‘control functionals’’, proceeds on the premise that the score function exists and can, in principle, be evaluated at any given point. We will leverage the score to construct more efficient estimators the expectation.
- Begin by splitting samples into two disjoint subsets, where the size of both subsets is assumed to increase linearly as n tends to infinity.
- The first subset is used to estimate a surrogate function, based on the gradient information contained in the score, such that the surrogate function shares the same expectation as but has a variance that vanishes as the size of the subset tends to infinity. This step is discussed in detail in the paper and can be easily facilitated using techniques from non-parametric regression.
- The second subset is used to evaluate an arithmetic mean.
- Any dependence on the split of the samples is then removed by averaging over many possible splits.
It is proven in the paper that the estimator that results from applying Steps 1-4 is (under weak regularity conditions) unbiased and achieves super-root-n convergence.
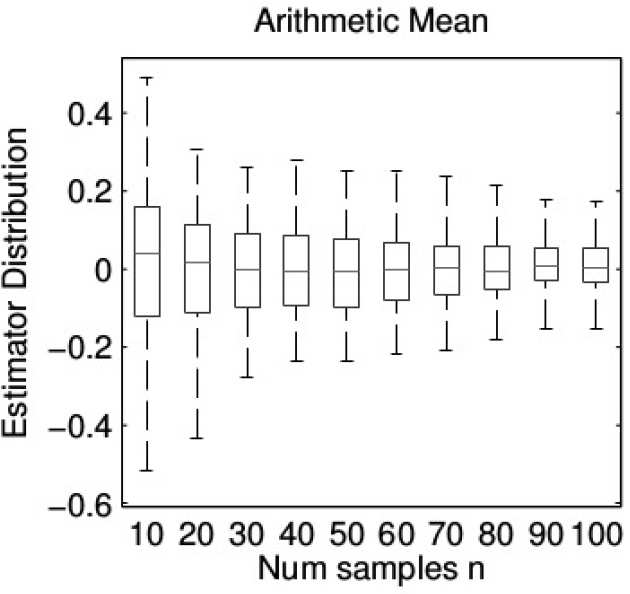
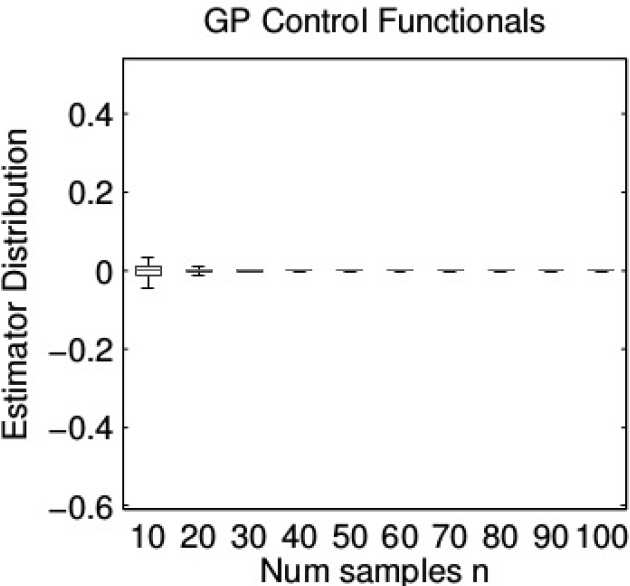
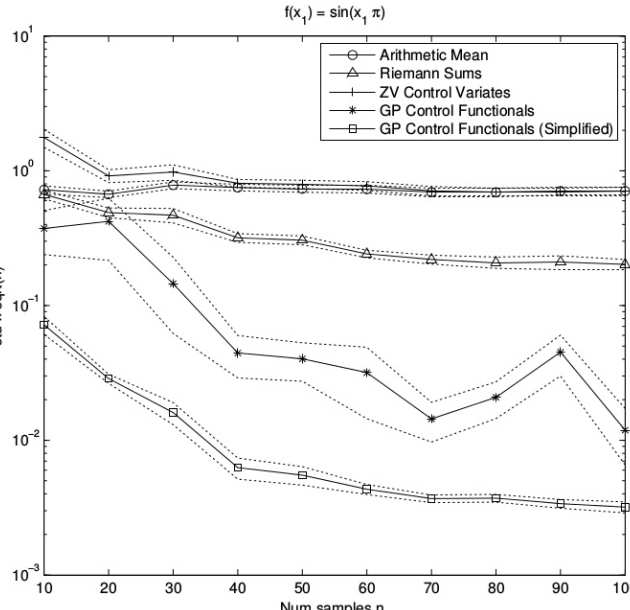
Results: Consider the toy example where f(x) = sin(πx) and X~N(0, 1). Here we know from symmetry that the expectation is zero. Applying the usual arithmetic mean estimator we obtain root-n convergence. Now contrast with the control functional estimator.This particular implementation estimates the surrogate function using techniques from Gaussian process (GP). The performance of control functionals is so strong that we need to use a different scale on the y-axis in order to compare the estimators. Here, on the y-axis we plot the (estimated) estimator standard deviation, multiplied by the square-root of n, so that the familiar root-n convergence is represented by a horizontal line.
You can see here that control functionals achieve super-root-n convergence. Here we also comare against “Riemann Sums” (DOI 10.1023/A:1008926514119) and “ZV Control Variates” (DOI 10.1007/s11222-012-9344-6). The difference between GP Control Functionals and GP Control Functionals (Simplified) is explained in the main text of the paper.
For further details, please refer to the full paper (link above), where you can also find applications of the control functional methodology to Bayes-Hermite quadrature, marginalisation in hierarchical models, and computation of normalising constants for non-linear differential equation models.
Reference: Oates, C. J., Girolami, M. and Chopin, N. (2017), Control functionals for Monte Carlo integration. J. R. Stat. Soc. B, 79: 695–718. doi:10.1111/rssb.12185
Related links
Convergence Rates for a Class of Estimators Based on Stein’s Method
This paper extends the paper “Control functionals for Monte Carlo Integration” by providing a detailed analysis of the convergence guarantees of control functionals when the target density and the integrand are both smooth. This helps further clarify scenarios in which the additional computational cost encurred by constructing control functionals will provide gains in statistical efficiency. Our results work both in the case of Monte Carlo i.i.d. samples from the target density, as well as some Markov chains with strong ergodicity properties.
Suppose the target density is a+1 times differentiable and the target integrand f is b+1 times differentiable. Under mild conditions on the integration domain, we show that the integration error of the corresponding control functional estimator converges at rate of \(O(n^{-\frac{1}{2} - min(a,b) / d + \epsilon})\), where n is the number of integrand evaluations and d is the dimension of the domain of integration. In cases where the target integrand and the target density are smooth, the control functional estimator will provide significant performance gains. The rate also highlights the curse of dimensionality which is common in control variates methods.
The paper concludes with some experiments on a challenging Bayesian inverse problem based on a PDE of steady-state flow in aquifers and other subsurface systems. These experiments demonstrate the potential gains attainable with control functionals.
Reference: Oates, C. J., Cockayne, J., Briol, F-X. & Girolami, M. (2016). Convergence Rates for a Class of Estimators Based on Stein’s Identity. arXiv:1603.03220.
Hamiltonian Monte Carlo
Geometry and Dynamics for Markov Chain Monte Carlo
Markov Chain Monte Carlo methods have revolutionised mathematical computation and enabled statistical inference within many previously intractable models. In this context, Hamiltonian dynamics have been proposed as an efficient way of building chains which can explore probability densities efficiently. The method emerges from physics and geometry and these links have been extensively studied by a series of authors through the last thirty years. However, there is currently a gap between the intuitions and knowledge of users of the methodology and our deep understanding of these theoretical foundations.
The aim of this review is to provide a comprehensive introduction to the geometric tools used in Hamiltonian Monte Carlo at a level accessible to statisticians, machine learners and other users of the methodology with only a basic understanding of Monte Carlo methods. This will be complemented with some discussion of the most recent advances in the field which we believe will become increasingly relevant to applied scientists.
Reference: Barp, A., Briol, F-X., Kennedy, A. D. & Girolami, M. (2017). Geometry and Dynamics for Markov Chain Monte Carlo. arXiv:1705.02891. Annual Review of Statistics and Its Applications, Vol. 5.
Riemann manifold Langevin and Hamiltonian Monte Carlo methods
This paper proposes Metropolis adjusted Langevin and Hamiltonian Monte Carlo sampling methods defined on the Riemann manifold to resolve the shortcomings of existing Monte Carlo algorithms when sampling from target densities that may be high dimensional and exhibit strong correlations. The methods provide fully automated adaptation mechanisms that circumvent the costly pilot runs required to tune proposal densities for Metropolis- Hastings or indeed Hamiltonian Monte Carlo and Metropolis Adjusted Langevin Algorithms. This allows for highly efficient sampling even in very high dimensions where different scalings may be required for the transient and stationary phases of the Markov chain.
The proposed methodology exploits the Riemannian geometry of the parameter space of statistical models and thus automatically adapts to the local structure when simulating paths across this manifold providing highly efficient convergence and exploration of the target density. The performance of these Riemannian Manifold Monte Carlo methods is rigorously assessed by performing inference on logistic regression models, log-Gaussian Cox point processes, stochastic volatility models, and Bayesian estimation of dynamical systems described by nonlinear differential equations. Substantial improvements in the time normalised Effective Sample Size are reported when compared to alternative sampling approaches.
Reference: Girolami, M. and Calderhead, B. (2011), Riemann manifold Langevin and Hamiltonian Monte Carlo methods. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 73: 123–214. doi:10.1111/j.1467-9868.2010.00765.x